从PageRank到CoRank

[TOC]

1 PageRank算法

1.1 算法来源

网页文本检索系统根据用户查询关键词与网页内容的相关程度来返回搜索结果，但是搜索结果未能体现页面的重要性。某些网页也可以通过堆砌关键词使自己的搜索排名靠前。于是，谷歌的两位创始人，当时还是美国斯坦福大学（Stanford University）研究生的佩奇（Larry Page）和布林（Sergey Brin）开始了对网页排序问题的研究。他们借鉴了学术界评判学术论文重要性的通用方法——论文的引用次数，于1998年提出了PageRank网页排序算法^[1]。PageRank算法的核心思想非常简单：

• 如果一个网页被很多其他网页链接到的话，说明这个网页比较重要，其PageRank值会相对较高

• 如果一个PageRank值很高的网页链接到一个其他的网页，那么被链接到的网页的PageRank值会相应地提高

如下图所示:

1.2 算法原理

互联网中的众多网页可以看作一个有向图。下图是一个简单的例子：

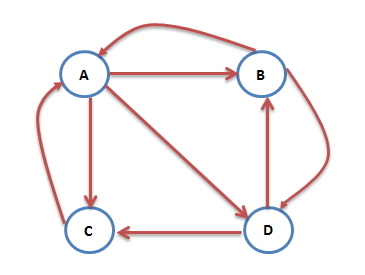
此时，A的PR值就可以表示为：

$$PR(A) = PR(B) + PR(C)$$

然而图中除了C之外，B和D都不止有一条出链，所以上面的计算式并不准确。想象一个用户现在在浏览B网页，那么下一步他打开A网页还是D网页在统计上应该是相同概率的。所以A的PR值应该表述为：

$$PR(A) = \frac{PR(B)}{2} + \frac{PR(C)}{1}$$

互联网中不乏一些没有出链的网页，如下图：

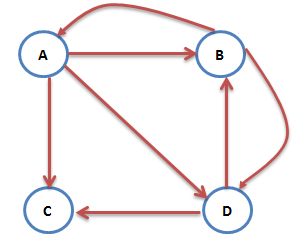
图中的C网页没有出链，对其他网页没有PR值的贡献，我们不喜欢这种自私的网页（其实是为了满足 Markov 链的收敛性），于是设定其对所有的网页（包括它自己）都有出链，则此图中A的PR值可表示为：

$$PR(A) = \frac{PR(B)}{2} + \frac{PR(C)}{4}$$

然而我们再考虑一种情况：互联网中一个网页只有对自己的出链，或者几个网页的出链形成一个循环圈。那么在不断地迭代过程中，这一个或几个网页的PR值将只增不减，显然不合理。如下图中的C网页就是刚刚说的只有对自己的出链的网页：

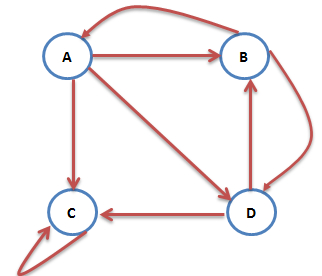
可以继续考虑以下几种情况:

1. 完全网络
2. 散点网络
3. 环网络
4. 悬挂节点

为了解决这个问题。我们想象一个随机浏览网页的人，当他到达C网页后，显然不会傻傻地一直被C网页的小把戏困住。我们假定他有一个确定的概率会输入网址直接跳转到一个随机的网页，并且跳转到每个网页的概率是一样的。于是则此图中A的PR值可表示为：

$$PR(A) = \alpha(\frac{PR(B)}{2}) + \frac{(1 - \alpha)}{4}$$

在一般情况下，一个网页的PR值计算如下：

$$PR(p_{i}) = \alpha \sum_{p_{j} \in M_{p_{i}}} \frac{PR(p_{j})}{L(p_{j})} + \frac{(1 - \alpha)}{N}$$

其中，$M_{p_i}$是网页$p_i$所有的入链网页集合，$L(p_j)$是网页$p_j$的出链数目，$N$是网页总数，$\alpha$一般取0.85。

此处可略过不看

(5)也可以表示为：

$$PR_{i}(t) = (1-c) \sum_{j=1}^n a_{ji}\frac{PR_{j}(t-1)}{k_{j}^{out}} + \frac{c}{n}$$

论文中还给出了一个简易计算方法：

$$PR(A) = (1-d) + d(\frac{PR(T_{1})}{C(T_{1})} + \dots + \frac{PR(T_{i})}{C(T_{i})})$$

PageRank算法总的来说就是预先给每个网页一个PR值（下面用PR值指代PageRank值），由于PR值物理意义上为一个网页被访问概率，所以一般是$\frac{1}{N}$，其中$N$是网页总数。因此，一般情况下，所有网页的PR值的总和为1（归一化）。如果不为1的话也可以，最后算出来的不同网页之间PR值的大小关系仍然是正确的，只是不能直接地反映概率了。预先给定PR值后，通过PageRank算法不断迭代，直至达到平稳为止。

1.3 算法证明

PageRank算法的证明主要包括两点，设$P_{n}$为第$n$次迭代时各网页PR值组成的列向量^[2]：

1. $\lim\limits_{n \to \infty}P_n$是否存在？
2. 如果存在，极限是否与$P_0$的选取无关？

为了方便证明，先将PR值的计算方法转换一下。仍然以上面例子来说：

可以用一个矩阵来表示这张图的出链入链关系，$S_{ij}=0$表示$j$网页没有对$i$网页的出链：

取$e$为所有分量都为 1 的列向量，定义矩阵：

$$A = \alpha S + \frac{(1 - \alpha)}{N}ee^T$$

则PR值的计算如下，其中$P_n$为第$n$次迭代时各网页PR值组成的列向量：

$$P_{n+1} = A^T P_{n}$$

于是计算PR值的过程就变成了一个Markov过程，PageRank算法的证明也就转为证明Markov过程的收敛性证明：如果这个 Markov 过程收敛，那么$\lim\limits{n \to \infty}P{n}$ 存在，且与$P_0$的选取无关。

若一个Markov过程收敛，那么它的状态转移矩阵$A$需要满足：

1. A为随机矩阵
2. A是不可约的
3. A是非周期的

第一点：随机矩阵又叫概率矩阵或 Markov 矩阵，满足以下条件：

$$令a_{ij}为矩阵A中第i行第j列的元素，则 \forall i = 1 \dots n, j = 1 \dots n, a_{ij} \geq 0, 且 \forall i = 1 \dots n, \sum_{j = 1}^n a_{ij} = 1$$

显然我们的$A$矩阵所有元素都大于等于0，并且每一列的元素和都为1。

第二点：方阵$A$是不可约的当且仅当与A对应的有向图是强联通的。有向图$G=(V, E)$是强联通的当且仅当对每一对节点对$u,v∈V$，存在从$u$到$v$的路径。因为我们在之前设定用户在浏览页面的时候有确定概率通过输入网址的方式访问一个随机网页，所以$A$矩阵同样满足不可约的要求。

第三点：所谓周期性，体现在Markov链的周期性上。即若$A$是周期性的，那么这个Markov链的状态就是周期性变化的。因为A是素矩阵（素矩阵(本原矩阵, 若一个n阶非负不可约矩阵(A的模=单特征值的个数)的单特征值个数为1，则称A为本原矩阵。)指自身的某个次幂为正矩阵的矩阵），所以A是非周期的。

至此，我们证明了PageRank算法的正确性。

1.4 算法设计

1.4.1 幂迭代法

首先给每个页面赋予随机的PR值，然后通过$P_{n+1}=AP_n$不断地迭代PR值。当满足下面的不等式后迭代结束，获得所有页面的PR值：

$$|P_{n+1} - P_{n}| < \epsilon$$

1.4.2 特征值法

当上面提到的Markov链收敛时，随机矩阵必有特征值1，且其特征向量所有分量全为正或全为负：

$$P = AP \Rightarrow P为矩阵A特征值1对应的特征向量$$

1.4.3 代数法

相似的，当上面提到的Markov链收敛时，必有：

$$\begin{equation}\begin{split} P = AP &\Rightarrow P = \lgroup \alpha S + \frac{(1 - \alpha)}{N}ee^T \rgroup P \\\\ 又&\because e为所有分量都为 1 的列向量，P的所有分量之和为1 \\\\ &\Rightarrow P = \alpha SP + \frac{(1 - \alpha)}{N}e \\\\ &\Rightarrow (ee^T - \alpha S)P = \frac{(1 - \alpha)}{N}e \\\\ &\Rightarrow P = (ee^T - \alpha S)^{-1} \frac{(1 - \alpha)}{N}e \end{split}\end{equation}$$

1.5 算法实现

对于以下网页关系:

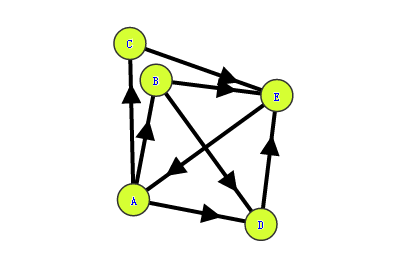
算法运行结果如下：

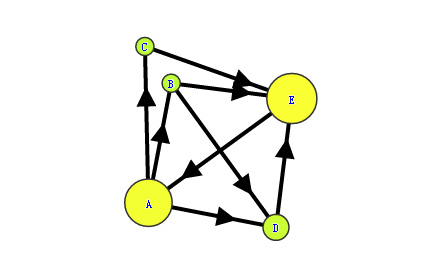
1.5.1 基于迭代的实现

使用Python基于python-graph-core库实现。

from pygraph.classes.digraph import digraph


class PRIterator:
    __doc__ = '''计算一张图中的PR值'''

    def __init__(self, dg):
        self.damping_factor = 0.85  # 阻尼系数,即α
        self.max_iterations = 100  # 最大迭代次数
        self.min_delta = 0.00001  # 确定迭代是否结束的参数,即ϵ
        self.graph = dg

    def page_rank(self):
        #  先将图中没有出链的节点改为对所有节点都有出链
        for node in self.graph.nodes():
            if len(self.graph.neighbors(node)) == 0:
                for node2 in self.graph.nodes():
                    digraph.add_edge(self.graph, (node, node2))

        nodes = self.graph.nodes()
        graph_size = len(nodes)

        if graph_size == 0:
            return {}
        page_rank = dict.fromkeys(nodes, 1.0 / graph_size)  # 给每个节点赋予初始的PR值
        damping_value = (1.0 - self.damping_factor) / graph_size  # 公式中的(1−α)/N部分

        flag = False
        for i in range(self.max_iterations):
            change = 0
            for node in nodes:
                rank = 0
                for incident_page in self.graph.incidents(node):  # 遍历所有“入射”的页面
                    rank += self.damping_factor * (page_rank[incident_page] / len(self.graph.neighbors(incident_page)))
                rank += damping_value
                change += abs(page_rank[node] - rank)  # 绝对值
                page_rank[node] = rank

            print("This is NO.%s iteration" % (i + 1))
            print(page_rank)

            if change < self.min_delta:
                flag = True
                break
        if flag:
            print("finished in %s iterations!" % node)
        else:
            print("finished out of 100 iterations!")
        return page_rank


if __name__ == '__main__':
    dg = digraph()

    dg.add_nodes(["A", "B", "C", "D", "E"])

    dg.add_edge(("A", "B"))
    dg.add_edge(("A", "C"))
    dg.add_edge(("A", "D"))
    dg.add_edge(("B", "D"))
    dg.add_edge(("C", "E"))
    dg.add_edge(("D", "E"))
    dg.add_edge(("B", "E"))
    dg.add_edge(("E", "A"))

    pr = PRIterator(dg)
    page_ranks = pr.page_rank()

    print("The final page rank is\n", page_ranks)

运行结果：

finished in 36 iterations!
The final page rank is
{'A': 0.2963453309000821, 'C': 0.11396451042168992, 'B': 0.11396451042168992, 'E': 0.31334518664434013, 'D': 0.16239975107315852}

1.5.2 基于MapReduce的实现

参考引用资料^[3]实现

# 暂无

1.6 算法的缺点

PR算法有几个缺点^[2]，这里我们主要关注其中一个：

算法规定从当前网页上随机跳转到下一个网页的概率都相同，然而这并不符合现实中人们的网页浏览方式，明显在内容丰富的网页上浏览时相比一个无趣的网页，人们跳转页面的概率大不相同。此外，随机最优参数$\alpha$的选取需要通过实验获得，对于不同的网络，参数的大小也不相同，不存在一个普遍参数。

2 LeaderRank算法

在许多在线社区中，用户可以选择其他用户作为他们的“意见领袖”。 我们通过一个网络来表示这些User—User关系，该网络具有从粉丝指向其领袖的有向链接，核心意见领袖会有大量的入链。目标是根据此网络拓扑对所有用户进行重要性排名。

为解决上述PageRank算法的缺点，在识别社交网络中高影响力用户时，吕琳媛等提出了改进的LeaderRank算法^[4][5]。通过向网络中增加一个与原网络所有节点双向链接“基准节点”，取代PageRank算法中人为指定的随机跳转概率参数，同时提高了算法的收敛速度。

2.1 算法思路

设想一个由 N 个节点和 M 个有向链路组成的网络G。节点对应用户，链接根据领袖和粉丝之间的关系建立。为了对用户进行排名，我们引入了一个“基准节点”，该节点通过双向链接连接到每个用户（见图2-1）。G因此变为了由$N+1$个节点和$M+2N$条边构成的强连通网络。为了开始排序过程，我们为除基准节点之外的每个节点分配一个分数单元，然后通过有向链接将其均匀分配给节点的指向节点。该过程一直持续达到稳定状态。

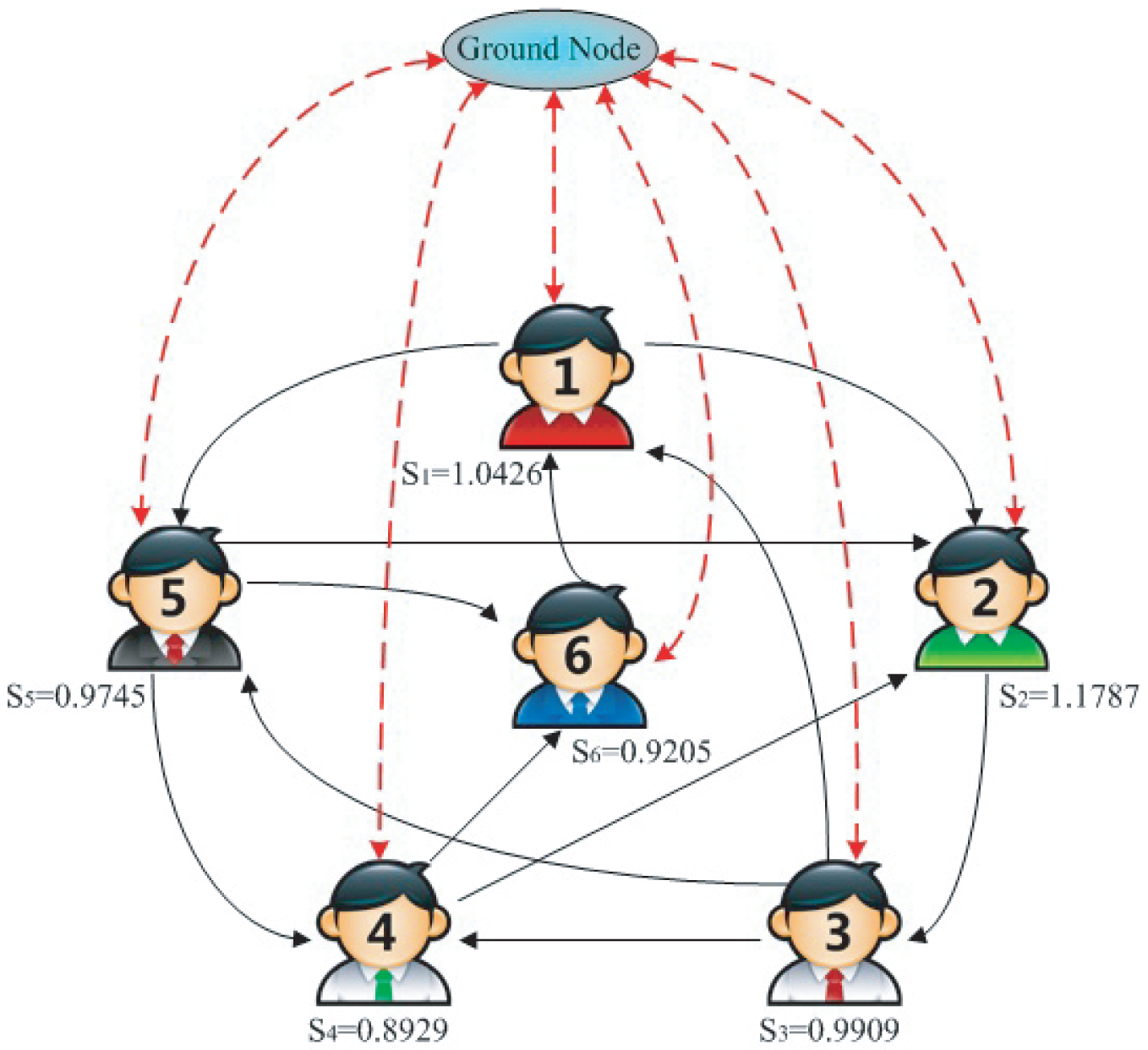
2.2 算法设计

数学意义上，这个过程相当于有向网络上的随机游走，并且该过程由随机矩阵 P 描述，其中元素$p{ij} = a{ij}/ki^{out}$ 表示随机游走者下一步从 i 走到 j 的概率。如果节点 i 指向 j，则$a{ij}=1$，否则为 0，$k_i^{out}$ 表示出度，即 i 的领袖数量。因此，这个概率流向可以看作粉丝 i 对领袖 j 的投票。

用$s_i(t)$表示节点 i 在时间 t 的得分，有：

$$s_{i}(t+1) = \sum_{j=1}^{N+1} \frac{a_{ji}}{k_{j}^{out}} s_{j}(t), \quad t=0, 1, 2, \dots, n.$$

初始分数规则：基准节点的$s_g(0)=0$，其它所有节点 i 的$s_i (0)=1$。

基准节点的存在使得 P 不可约，因为网络是强连通的。基准节点还确保任何节点的大小为 2 和 3 的环路共存，这意味着 $P^6$ 为正，即 $P^6$ 的所有元素都大于零。由于 $P^n$ 对某些自然数 n 为正，因此 P 是和非负基元矩阵。根据 Perron-Frobenius 定理，P 具有最大特征值 1 和唯一特征向量。

因此，所有 i 的分数 $s_i(t)$ 将收敛到唯一的稳定状态，表示为 $s_i(t_c)$，其中 $t_c$ 是收敛时间。在稳定状态下，我们将基准节点的分数平均分配给所有其他节点。用户 i 的最终影响力得分S，即：

$$S_i = s_i(t_c) + \frac{s_g(t_c)}{N}$$

其中，$s_g(t_c)$是基准节点在稳态时的得分。

2.3 算法优点

基于上述特性，在排名中应用 LeaderRank 有几个优点，包括：

1. 无参数
2. 广泛适用于任何类型的图
3. 收敛到唯一的排名序列
4. 初始条件的独立性

2.4 算法实现

% This is a Matlab M−file for LeaderRank.

E=load('Network.dat'); % Read the network data with different pairs
													% of 'fan leader' in consecutive rows, and  the
													% labels of nodes should start from 1
l=length(E);						% l is the number of links
N=max(max(E));					% N is the number of nodes.

% Add ground node and create adjacency matrix P
EG1=zeros(N, 2);	% N rows 2 cols
EG2=zeros(N, 2);
for i=1:N
		EG1(i, 1)=N+1;
		EG1(i, 2)=i;
end
EG2(:, 1)=EG1(:, 2);
EG2(:, 2)=EG1(:, 1);
E=[E; EG1; EG2];
P=sparse(E(:, 1), E(:, 2), 1);
D_in=sum(P);		% in degree
D_out=sum(P');	% out degree

% Transition matrix PP
EE=zeros(N+1, 2);
for j=1:N+1
		EE(j, 1)=j;
		EE(j, 2)=1/D_out(j);
end
D=sparse(EE(:, 1), EE(:, 1), EE(:, 2));
PP=D∗P;

% Diffusion to stable state.
God=zeros(N+1, 1);
God(1:N, 1)=1;								% Assign initial resource
error=10000;									% error is the average error of nodes' scores.
error_threshold=0.00002;			% It is a tunable parameter controlling the
																% error tolerance.
step=1;
while error>error_threshold
		step
		M=God;
		God=PP'∗God;							% P' means the transpose of P
		error=sum(abs(God−M)./M)/(N+1);
		step=step+1;
end
b=God(N+1)/N;
God=God+b;
God(N+1)=0;

% Write the ranking results to "Results.dat": node's ID & Score
R=zeros(N, 2);
R(:, 1)=[1:N]';
R(:, 2)=God(1:N);
[b, pos]=sort(−R(:, 2));
R=R(pos, :);
fid=fopen('Results.dat', 'w');
for i=1:N
		fprintf(fid, '%d%f\n', R(i, 1), R(i, 2));
end
fclose(fid);

3 CoRank算法

3.1 算法构思

3.2 子算法设计

3.2.1 基础属性重要性算法

$$w_{bp} = |\vec x| = \sqrt{x_1^2+x_2^2+\dots+x_n^2}$$

模长 or 特征向量中心性？

3.2.2 基于临域相似度的节点核心度算法

$$\begin{align} LLS(i) &= \sum_{a, b \in n_i} (1-sim(a,b)) + c \notag \\ &= k_i - \sum_{a, b \in n_i} sim(a, b) + c \\ \end{align}$$

$if \qquad sim(a,b) = 1 \qquad then \qquad c = \frac {2}{n_i(n_i-1)} \notag \qquad else \qquad c = 0$

3.2.3 节点综合情感权重算法

$$w_{ji} = \frac{\sum (e_{ji}^{pos}-e_{ji}^{neg})}{n_{ji}} + r_{ji}$$

其中，$w{ji} \in [-1, 1]$，为节点$j$对节点$i$的综合情感权重；$r{ji}$为节点是否互为好友；如果$i=g$, 则$w_{jg} = 0$。

3.2.4 CoRank 核心用户识别算法

使用用户$i$到$j$的综合情感倾向作为节点间的有向边权重，生成状态转移矩阵，Ground节点与其它所有节点间的权重均为 1 均值

i指向g时，w取i指出去的所有值的均值，g指向i时，w为1/N

$$s_{i}(t+1) = \sum_{j=1}^{N+1} \frac{w_{ji}}{\sum_{l=1}^{N+1}w_{jl}^{out}} s_{j}(t), \quad t=0, 1, 2, \dots, n.$$ $$S_i = s_i(t_c) + \frac{s_g(t_c)}{N}$$

负值乘以负权重？怎么传递？还是平移量纲？

平移量纲，使得$w_e \in [0, 2]$，如果$i=g$, 则$w_e = 1$。

以式（16）和（17）的结果归一化后求和，初始化CR向量

$$CR_1 = [cr_1^1, cr_2^1, \dots , cr_n^1]^{T} \\ 迭代n次后的结果 \\ CR_n = [cr_1^n, cr_2^n, \dots , cr_n^n]^{T}$$

以情感分析结果和式（18）构造状态转移矩阵

$$A$$

则

$$CR_{n+1} = ACR_{n}$$

3.2.5 数据的标准化和归一化方法

• Min-Max归一化

  $$X_{norm} = \frac{X_i-X{min}}{X_{max}-X_{min}}$$

• 均值标准化

  $$X_{std} = \frac{X_i-\mu}{\sigma}$$

3.3 算法实现A->B: 一样效果

A->B: react

参考资料

1. BRIN S, PAGE L. The anatomy of a large-scale hypertextual Web search engine[J]. Computer Networks and ISDN Systems, 1998, 30(1–7): 107–117. DOI:10.1016/s0169-7552(98)00110-x. ↩
2. PageRank算法从原理到实现 ↩
3. Using MapReduce to compute PageRank ↩
4. LÜ L, ZHANG Y-C, YEUNG C H, et al. Leaders in Social Networks, the Delicious Case[J]. PLoS ONE, 2011, 6(6): e21202. DOI:10.1371/journal.pone.0021202. ↩
5. LeaderRank ↩